FP試験の6つの係数問題　おぼえずに解く方法

FP試験の1級や2級の学科試験で出題される6つの係数問題には、問題文に係数の数値が与えられる出題パターンがあります。

このパターンの問題については、係数の意味をまったく理解していなくても、係数の数値をよく見れば解くことができます。

しかも、FP1級のきんざいの学科試験（基礎編）では、これまでの傾向から係数の数値が与えられる出題パターンしかないため、1級でも使えるテクニックになります。

この記事ではFP3級～1級すべて一発合格した筆者が、FP試験に出題される6つの係数を問題文の係数の数値だけで解く方法を解説します。

「減債基金係数と資本回収係数の見分け方だけを知りたい」という方のために、後半の「減債基金係数と資本回収係数の選択肢で迷ったとき」の項目で簡単に見分る方法をまとめました。ぜひご活用ください。

6つの係数問題の出題頻度と出題パターン
係数問題を係数の意味を覚えずに解く方法
減債基金係数と資本回収係数の選択肢で迷ったとき
FP1級の問題も覚えずに解ける
【注意】係数を覚えない方法で解けない問題もある
直前でも間に合う！全級一発合格者がおすすめする問題集

目次へ

6つの係数問題の出題頻度と出題パターン

係数問題には、問題文で係数が与えられるパターンと係数が与えられないパターンがあります。それぞれの出題頻度は下記のとおりです。

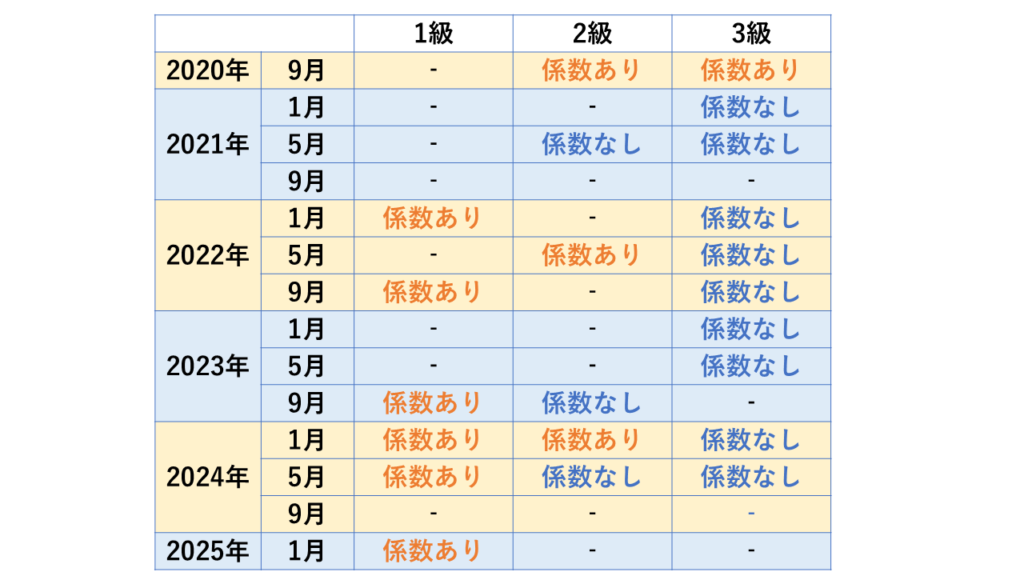
【表について】金融財政事情研究会（以下、きんざい）と日本FP協会が公開している、学科試験（50問の択一式）の過去問から筆者が独自にまとめています。1級の学科試験はきんざいの基礎編のみでの実施となりますので、1級はきんざい、2級・3級はきんざいとFP協会の両方が対象になっています。（2020年9月と2021年1月はきんざいのみで確認）

（参考）金融財政事情研究会：試験問題

（参考）日本FP協会：試験問題・模範解答

上記のとおり、1級なら毎回、2級は2回に1回程度、問題文で係数が与えられることがわかります。

この記事で解説する、6つの係数を覚えなくても解く方法が使えるのは、係数が与えられる問題のみです。

係数なし問題の対策について

FP2級・3級の試験では係数が与えられない問題の対策も必要になります。

6つの係数を覚える方法についてはこちらの記事で解説しています。

もう忘れない！FP試験の6つの係数の名前と意味を覚える方法

係数問題を係数の意味を覚えずに解く方法

それでは実際に出題されたFP2級の過去問を使って、解き方の手順を解説します。

下記は、日本FP協会の2級の学科試験（2022年5月分）の問題です。

（出典）：日本FP協会 2級ファイナンシャル・プランニング技能検定学科試験2022年5月

手順1：元本の増減に着目して選択肢を分別する

まずは4つの選択肢をすべて読み、元本の増減があるものと、ないものに分けます。

元本の増減があるものとは、「毎年積み立てる」とか「毎年受け取る・取り崩す」というような行動によって、が運用期間の途中で元本が増えたり減ったりするものをいいます。

例題では、選択肢2と3にその表現があります。

【選択肢2】年率2％で複利運用しながら10年後に100万円を得るために必要な毎年の積立額は「100 万円×0.0913」で求められる。

【選択肢3】10年間にわたり、年率2％で複利運用しながら、毎年100万円を受け取るために必要な元本は「100万円×10.9497」で求められる。

問題を解く時は、この表現がない選択肢から先に解きます。

手順2：元本の増減がないものを解く

それでは選択肢1と4から解きます。選択肢1から見ていきます。

【選択肢1】元本100万円を10年間にわたり、年率2％で複利運用した場合の元利合計額は「100万円×1.2190」で求められる。

この選択肢は、「元金100万円を年利2％で10年間、複利運用した後の元利合計（元金＋利息）」を求める内容です。

問題文に「毎年積み立てる」とか「毎年受け取る・取り崩す」といった表現がないので、最初に投入した100万円から元本が変わらないことがわかります。

参考：複利運用とは

複利運用とは、利息計算の対象となる元金に、それまでの利息を含めて計算する運用方法のことです。

【例：元金100万円、年利2％】

・1回目の利息：100万円×2％（2万円）

・2回目の利息：102万円×2％（2万400円）

・3回目の利息：104万400円×2％（2万808円）

それでは、この問題文を図でイメージしてみましょう。

次のような右肩上がりの棒グラフで表すことができます。

100万円にどの係数を乗じれば、複利運用した後の元利合計を算定できそうでしょうか。数字の大きさだけを見比べて当ててください。

1.2190	終価係数
0.8203	現価係数
10.9497	年金終価係数
0.0913	減債基金係数
8.9826	年金現価係数
0.1113	資本回収係数

この問題は、運用した後の元利合計が100万円を超えることに気づけるかどうかがポイントです。

年利2％で運用しているため、10年後は元本である100万円を超えなければおかしくなります。

そのため、1以下の係数（現価係数・減債基金係数・資本回収係数）は、正しくないことがわかります。

続いて、元金が100万円から変わっていないことに注目します。

たった10年運用しただけで900万円近くになる「8.9826」や1,000万円を超える「10.9497」の係数では、明らかに数値が大きすぎます。

確信がもてないときは、数年分の利息を試験問題の端などで計算してみましょう。

100万円に対する年利2％では初年度の利息は2万円、2年目の利息は102万円の2％で2万400円です。

そうすると「このペースの利息をたった10回受け取ったくらいで、元金が100万円から800万円や1,000万円になるはずがない」と自信をもって判断できます。

したがって、ちょうどいい係数は消去法で「1.2190」（終価係数）しかありません。この選択肢は「〇」です。

【参考：終価係数の計算方法】

・利息：年2％

・運用期間：10年

　→　1.02＾9乗＝1.21899…

続いて、元本の増減がないもう一つの選択肢も見ていきましょう。

【選択肢4】年率2％で複利運用しながら10年後に100万円を得るために必要な元本は「100万円×0.8203」で求められる。

これもイメージ図にしてみましょう。

元本が変わらないため、イメージ図は【選択肢1】とまったく同じです。

ただし、求める金額は【選択肢1】の逆で、【選択肢4】は運用する前の元金を求める問題になっています。

100万円にどの係数を乗じれば、運用開始前（10年前）の元金になりそうでしょうか。数字の大きさだけを見比べて当ててください。

1.2190	終価係数
0.8203	現価係数
10.9497	年金終価係数
0.0913	減債基金係数
8.9826	年金現価係数
0.1113	資本回収係数

毎年の複利によって増え続けた10年後の運用結果が100万円であるため、運用する前の元金は100万円より小さくなるはずです。そのため、係数の数値は「1未満」のものになります。

しかし、「0.0913」や「0.1113」では、元金が10分の1ほどになります。10万円を年利2％で運用してみて、それが10年後に10倍の100万円になることはありえません。

元金が運用中に増えていないため、利息年2％で100万円を貯めるには、100万円に近い元金が必要になります。

条件に合う係数は「0.8203」の現価係数しかありませんので、この選択肢は「〇」です。

【参考：現価係数の計算方法】

・利息：年2％

・運用期間：10年

　→　1÷1.02＾9乗（＝1／終価係数）

筆者

元本の増減がないものから解く理由は、数値をイメージしやすいからです。ここで正答（誤った選択肢）を見つけることができればラッキーなので先に解くことをおすすめしています。

手順3：毎年積み立てる・毎年受け取る選択肢を解く

それでは、元本の増減がある選択肢を解いてみましょう。

「毎年積み立てる」とか「毎年受け取る・取り崩す」といった表現のある選択肢のことです。

それぞれに出題パターンが2つずつあります。

ここからの解説は、まずは「毎年積み立てる問題【パターン1】・【パターン2】」、そして最後に「毎年受け取る問題【パターン1】・【パターン2】」の順番で行います。

毎年積み立てる問題【パターン1】

それでは、「毎年積み立てる問題」から解説します。

ちょうどよい問題文の選択肢がなかったので、筆者で問題文を追加します。

【筆者で追加】毎年100万円を積み立てながら、年率2％で複利運用した場合の元利合計額は「100万円×〇〇」で求められる。〇〇にあてはまる係数を6つから選びなさい。

この選択肢は、毎年100万円を積み立てながら、10年間運用した後の元利合計を求める問題になります。

毎年100万円の元金を10年（＝10回）で積み上げていくため、上り階段のようなイメージになります。

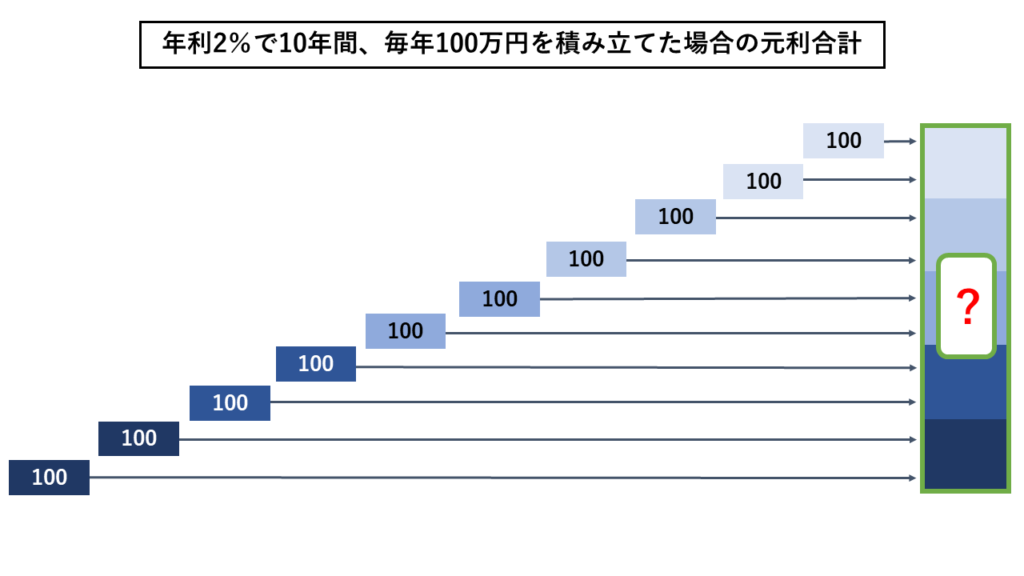
100万円にどの係数を乗じれば、10年後の元利合計になりそうでしょうか。数字の大きさだけを見比べて当ててください。

1.2190	終価係数
0.8203	現価係数
10.9497	年金終価係数
0.0913	減債基金係数
8.9826	年金現価係数
0.1113	資本回収係数

この問題は、運用後の将来の元利合計が1,000万円を超えることに気づけるかどうかがポイントです。

求めるのは運用した後の将来の元利合計ですが、元金だけで考えてみましょう。

10年間で100万円ずつ積み立てた場合、元本のトータルは1,000万円ですから、少なくとも10年後の元利合計は1,000万円を超えなければおかしいことになります。

言い換えると、運用年数である「10」を超える倍率でなければおかしいのです。

したがって、「10.9497」の「年金終価係数」しかありません。

【参考：年金終価係数の計算方法】

・利息：年2％

・運用期間：10年

　→　1+(1+0.02)+(1+0.02)^2乗+・・・+(1+0.02)^9乗

毎年積み立てる問題【パターン2】

続いては、積み立てる問題の2つめのパターンとなる、1年あたりの積み立て額を求める選択肢です。再び過去問に戻ります。

【選択肢2】年率2％で複利運用しながら10年後に100万円を得るために必要な毎年の積立額は「100 万円×0.0913」で求められる。

この選択肢では、10年後に100万円を貯めるための1年あたりの積み立て額を計算しようとしています。

次の図のようなイメージになります。

100万円にどの係数を乗じれば、1年あたりの積み立て金額になりそうでしょうか。数字の大きさだけを見比べて当ててください。

1.2190	終価係数
0.8203	現価係数
10.9497	年金終価係数
0.0913	減債基金係数
8.9826	年金現価係数
0.1113	資本回収係数

係数の数値は「1未満」になります。

しかし、「0.8203」では数が大きすぎます。10回で100万円を積み立てればいいのに、1年で約82万円（100万円×0.8203）も積み立てたら10年後は明らかに100万円をオーバーします。

したがって「0.0913」か「0.1113」の2択となります。

それでは、100万円を10年かけて積み立てるために、1年あたり10万円の積み立てが必要でしょうか。

答えは必要ありません。積み立てている間に利息がつくからです。

したがって答えは、「0.0913」の減債基金係数になりますので、選択肢は「〇」です。

【参考：減債基金係数の計算方法】

　→　現金終価係数の逆数になります

減債基金係数は文章だけでは理解しづらいです。次項の「減債基金係数と資本回収係数の選択肢で迷ったとき」で今の説明を図解していますので、ぜひご活用ください。

毎年受け取る（取り崩す）問題【パターン1】

それでは「毎年受け取る問題」の解説をします。過去問の【選択肢3】を解いてみましょう。

【選択肢3】10年間にわたり、年率2％で複利運用しながら、毎年100万円を受け取るために必要な元本は「100万円×10.9497」で求められる。

この選択肢は、年利2％で元金を運用しながら、そこから10年間、毎年100万円を受け取りたい場合に、受け取り開始前に用意しておかなければならない元金を求める問題になります。

年金100万円を10年（＝10回）引き出す問題なので、下り階段のようなイメージになります。

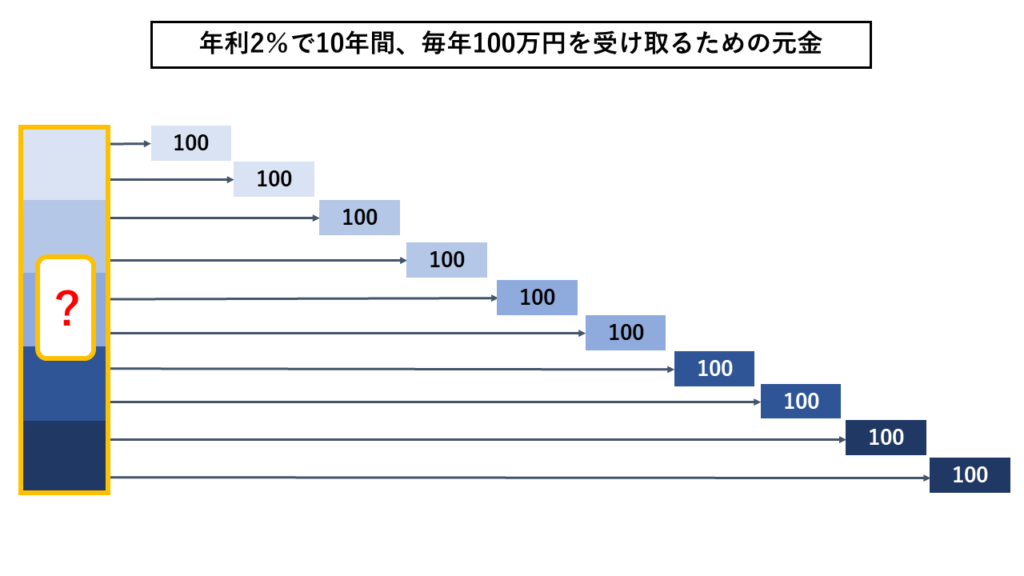
100万円にどの係数を乗じれば、受け取り開始前の元本になりそうでしょうか。数字の大きさだけを見比べて当ててください。

1.2190	終価係数
0.8203	現価係数
10.9497	年金終価係数
0.0913	減債基金係数
8.9826	年金現価係数
0.1113	資本回収係数

この問題では、年金100万円を10年（＝10回）引き出すため、受け取りたい金額のトータルは1,000万円になります。

利息は年2％しかないため、受け取り開始前の元本も、これに近い金額が必要になります。

数値が1未満の係数や、1を超えていても値が小さい係数は、答えに当てはまりません。したがって、「10.9497」か「8.9826」に絞ることができます。

それでは、受け取りたい金額のトータルが1,000万円であるからといって、受け取り開始前の元本が1,000万円も必要になるでしょうか。

ポイントは、年100万円ずつ受け取る間にも、まだ取り崩していない元本の複利運用が続いていることです。

年100万円を受け取っている間も残りの元本が利息で増加するため、受け取り開始前の元本は1,000万円も要らないことになります。

言い換えると、運用年数である「10」を超える倍率になることはありません。

したがって「10.9497」は「10倍」を超えるため当てはまりません。答えは「8.9826」の「年金現価係数」ですので、この選択肢は「✕」です。

【参考：年金現価係数の計算方法】

・利息：年2％

・運用期間：10年

　→　1/(1+0.02)+1/(1+0.02)^2乗+・・・+(1+0.02)^10乗

毎年受け取る問題【パターン2】

最後は「毎年受け取る問題」の2つめの出題パターンです。1年あたりの「受け取り額」を計算する問題になります。問題文は筆者で追加しています。

【筆者で追加】100万円を年率2％で複利運用しながら、10年間にわたって毎年均等額を受け取る場合、毎年の受け取り額は「100万円×〇〇」で求められる。

この選択肢では、100万円を運用しながら、10年間、毎年同じ額を受け取りたい場合、1年間にいくら取り崩せるかという問題です。

100万円にどの係数を乗じれば、1年あたりの受け取り金額になりそうでしょうか。数字の大きさだけを見比べて当ててください。

1.2190	終価係数
0.8203	現価係数
10.9497	年金終価係数
0.0913	減債基金係数
8.9826	年金現価係数
0.1113	資本回収係数

係数の数値は「1未満」になりますが、「0.8203」では数が大きすぎます。1年で約82万円（100万円×0.8203）も受け取ったら、翌年にはもう取り崩せるお金はなくなっています。

したがって「0.0913」か「0.1113」の2択となります。

もうお分かりと思います。答えは「0.1113」の資本回収係数です。

なぜなら、100万円を10年間にわたって取り崩している間も、元本は運用をされており増え続けていますから、1年あたりの受け取り額は10万円を超えなければおかしいのです。

【参考：資本回収係数の計算方法】

　→　年金現価係数の逆数になります

資本回収係数もまた、文章だけでは理解しづらいです。次項の「減債基金係数と資本回収係数の選択肢で迷ったとき」で今の説明を図解していますので、ぜひご活用ください。

減債基金係数と資本回収係数の選択肢で迷ったとき

減債基金係数と資本回収係数は、数値が近いため区別が難しく、試験でも狙われやすいところです。

もし、どちらが「積み立て」でどちらが「受け取り」であるかを思い出せなくなったときは、次の方法で試験中に思い出すことができます。

利息がない場合を想像してみる

積み立てや受け取りに利息が一切つかないと仮定した場合に、どうなるのかを考えてみましょう。

もし、現金をまったく運用せず利息が一切つかない場合、1年あたりの積み立て額と受け取り額の計算はとてもシンプルで、どちらも「1÷運用年数」になります。

たとえば、50万円を5年で積み立てるための年額は「5分の1（0.2）」で10万円、50万円を5年で均等に取り崩す額も「5分の1（0.2）」で10万円のように、かなりシンプルになります。

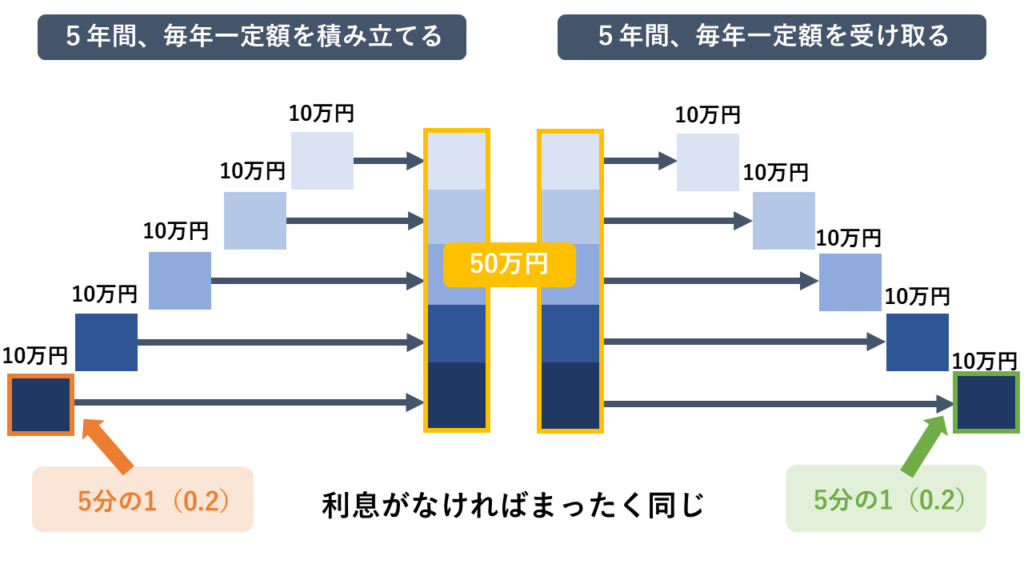
これを踏まえて、どちらが積み立てでどちらが受け取りになるかを考えてみましょう。

積み立てる額は利息がつく前の金額なので1年分は5分の1（0.2）よりも小さく、受け取る額は元金Max状態からの利息を上乗せした後の金額なので5分の1（0.2）よりも大きくなるはずです。

つまり、問題文が「積み立て」ならその係数は「1÷運用年数」よりも小さい値に、「受け取り」なら係数は「1÷運用年数」よりも大きい値になります。

先ほどの過去問の減債基金係数は「0.0913」、資本回収係数は「0.1113」で、運用年数は10年でした。したがって「0.1」を挟んで、小さいほうが積み立て、大きいほうが受け取りになります。係数の名前は覚えてなくてよいです。

言葉の連想で覚える

試験中にど忘れすることは誰にでもありますから、もう一つ、減債基金係数と資本回収係数の覚え方をご紹介します。

減債基金係数にある「基金」には、国民年金基金など「年金の積み立て」をイメージしやすい言葉が含まれています。これを活用して「基金＝積み立て」で思い出せるようにしておくとよいでしょう。

資本回収係数の「回収」についても、「受け取って回収する」という問題文の状況に結び付けることができます。

FP1級の問題も覚えずに解ける

6つの係数が与えられる問題

近年の過去問を見る限り、1級の問題は6つの係数が与えられています。

したがって、この記事のテクニックを使って問題を読み取れば、係数の意味を覚えていなくても解けます。

さっそくチャレンジしてみましょう。

（出典）一般社団法人金融財政事情研究会ファイナンシャル・プランニング技能検定1 級学科試験（基礎編）2023年9月

この問題は、将来、毎年100万円を10年受け取るために、今から20年かけて一定額を積み立てる場合の1年あたりの積み立て額を求める問題です。

筆者は1級の試験勉強をしていて、このパターン以外の出題を見たことがありません。

おそらくこの問題が解ければ、現状では対策は十分といえると思います。

この問題を図にすると下記のようになります。

運用しながら100万円を受け取るというゴールから、これから毎年積み立てていく1年あたりの金額を「2つの係数」を使って逆算すれば解くことができます。

必要な知識は2級と変わりません。

まずは図の右半分に注目して、毎年の受け取り金額100万円から「取り崩し前の元金」（真ん中の元金Maxの状態）を求めます。

受け取り期間は10年ですので、運用期間10年の6つの係数を見ます。

1.3439	終価係数
0.7441	現価係数
11.4639	年金終価係数
0.0872	減債基金係数
8.5302	年金現価係数
0.1172	資本回収係数

100万円を10年間受け取るので、受け取り金額はトータルで1,000万円です。しかし、途中で運用利息が入るため、元金は1,000万円も必要ありません。

したがって100万円に乗じるちょうどよい係数は「8.5302」（年金現価係数）になり、取り崩し前の元金は「853万200円」あればよいことがわかります。

次は、この「853万200円」を20年かけて貯めるための、1年あたりの積み立て額を求めます。

次は運用期間20年の6つの係数を見ます。

1.8061	終価係数
0.5537	現価係数
26.8704	年金終価係数
0.0372	減債基金係数
14.8775	年金現価係数
0.0672	資本回収係数

迷う係数は、減債基金係数と資本回収係数です。

ここで「1÷20年」をして「0.05」を出します。

これから積み立てる1年あたりの金額は、利息がつく前ですので「0.05」よりも小さい係数になります。

したがって「853万200円」に乗じる係数に該当するのは「0.0372」（減債基金係数）になります。

よってこれから積み立てる1年あたりの金額は、317,323円になります。一番近い選択肢1が正解です。

減債基金係数と資本回収係数が与えられない場合

最近の過去問では見かけませんが、ひと昔前までは、1級の過去問として減債基金係数と資本回収係数を与えず4つの係数（難しい時は3つ）から解かせる問題がありました。

この場合、減債基金係数と年金終価係数、年金現価係数と資本回収係数の逆数関係を利用して、減債基金係数と資本回収係数を自力で算定しなければなりません。

逆数関係とは、お互いを乗じると「1」になる関係のことです。例えば年金現価係数が6だった場合、資本回収係数が6分の1になるというような関係をいいます。

6つの係数は、下記の組み合わせで逆数関係になっています。

現価係数	終価係数
減債基金係数	年金終価係数
年金現価係数	資本回収係数

減債基金係数は「1÷年金終価係数」、資本回収係数は「1÷年金現価係数」によって計算できます。

逆数関係を確かめたい場合は、先ほどの答えである1年あたりの金額を逆数で年100万円に戻してみましょう。

先ほどの解答は1年あたり317,323円でした。

これに年金終価係数（20年：26.8704）と資本回収係数（10年：0.1172）を乗じると、999,317円になります。（ズレは係数の端数処理によるもの）

【注意】係数を覚えない方法で解けない問題もある

この記事で紹介した、係数を覚えずに解くテクニックを使って解けない問題が2つあります。

係数の数値が与えられない問題

最初にお伝えしたとおり、FP3級や2級の試験には、6つの係数の値が与えられない問題が出題されることがあります。

その場合は、係数の大きさをだけで解いていく今回のテクニックは残念ながら通用しません。

利回り・運用年数が高すぎる問題

こちらはあまり心配はないのですが、利回りや運用年数があまりに高い問題の場合、6つの係数の大きさに逆転が生じますので、係数の大きさのみの比較で解くことができなくなります。

先ほどの問題では、年利2％で10年の運用を前提としていましたが、これが年利10％や25％になると、下記のようになります。

上図の年利25％で、中間の4つの係数の数値の大きさが逆転しているのが見えますでしょうか。

このように利回りがあまりに大きくなると上図の同じ色の係数の差が広がり、両端の係数の差が広がる一方で、中間の4つの係数の値が近くなります。そして、一定値を超えると逆転します。運用年数10年であれば利回り16％を超えたあたりで各係数の値が逆転してしまいます。

ただし、確認できる範囲の過去問では、年利1％～5％の範囲で出題されていますので、それほど心配はいりません。FP試験での6つの係数はライフプランニングの資産形成の分野になりますので、堅実な提案が求められます。そのため、ハイリスク・ハイリターンな運用で資産形成をさせるような問題は、おそらく出題しづらいのだと思います。

新NISA（恒久NISA）の登場で、今後、問題文の運用年数を上げてくることが考えられます。

参考までに、年利5％・運用年数50年の「ハイリターン＆超長期運用」の係数を試算してみました。下記のとおり、係数の逆転は発生しませんでしたが、だいぶ数値が乱れていますので、この組み合わせを限界ラインの目安にするとよいでしょう。

11.4674	終価係数
0.0872	現価係数
209.3480	年金終価係数
0.0048	減債基金係数
18.2559	年金現価係数
0.0548	資本回収係数

利回り5％・運用年数50年

このような「ハイリターン・超長期運用」の問題が今後出題されるようになれば、終価係数と年金現価係数、あるいは現価係数と資本回収係数の取り違えを防止するために、最初に「積み立て・受け取り用の係数」として、運用年数の「50」を挟んだ「209.3480」と「18.2559」と、運用年数「1/50年」の「0.02」を挟んだ「0.0548」と「0.0048」の数値を、ピックアップしておくと良いと思います。