FP3級や2級の学科試験に出題される6つの係数問題には、問題文を読んで「知りたい金額」と、「それを計算するために必要な係数」の正しい組み合わせ(あるいは誤った組み合わせ)を選ぶ問いが出題されます。
この問題を解くためには、6つの係数のそれぞれの「名称」と「意味(どんな時に使うのか)」を結びつけて覚えることが必要です。
しかし、6つの係数は説明がよく似ており区別が難しく、丸暗記と非常に相性が悪いといえます。
この記事ではFP3級~1級すべて一発合格した筆者が実際に使った、6つの係数の覚え方を解説します。
これから6つの係数の覚え方を解説します。「丁寧な解説は不要!」という方は、最後の「総まとめ」で覚え方を簡単にまとめました。ぜひご活用ください。
6つの係数問題の出題パターン
6つの係数問題の出題パターンは、「係数あり」と「係数なし」の2つのパターンに分類することができます。
「係数あり」とは問題文で係数の数値が与えられる問題のことで、「係数なし」とは係数の数値が与えられない問題のことをいいます。
この2つのパターンのうち、「係数なし」の問題については、係数の名称と意味の組み合わせを覚えていなければ解くことができません。
それでは先ほどの表で、6つの係数問題の出題パターンを確認してみましょう。
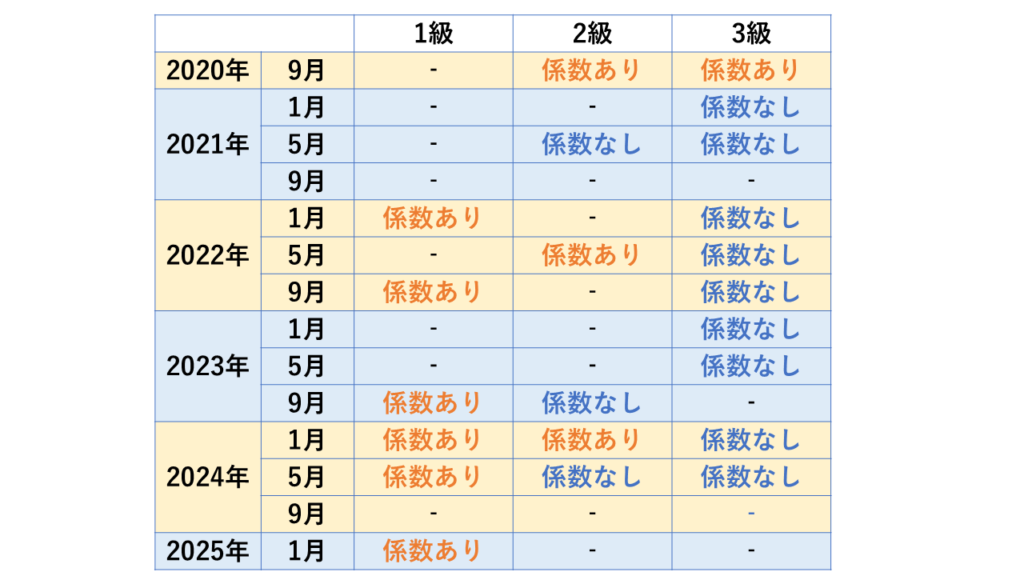
ご覧のとおり、3級試験や2級試験における6つの係数問題では「係数なし」が出題されます。
「係数なし」を解くためには、各係数の「名称」と「意味(どんな時に使うのか)」を結び付けて覚えることが欠かせません。
一方、係数が問題文で与えられる「係数あり」については、係数の意味をまったく覚えていなくても数値から答えを推理して解くテクニックがあります。
覚えなくてよいため勉強は楽ですが、係数が与えられなかった場合は使えません。
参考までにこちらの記事で解説しています。
各係数の意味を覚えれば、「係数あり」と「係数なし」のすべての問題に対応できるようになります。そのため、各係数の「名称」と「意味」を覚える方法がおすすめです。
本記事では、6つの係数を丸暗記せずに覚えられる方法を紹介します。
6つの係数の覚え方
6つの係数の「名称」と「意味(どんな時に使うのか)」の組み合わせを、丸暗記をせずに覚えるためには、6つの係数を、次の3つの“特徴”を使って覚える方法がおすすめです。
・知りたい金額は現在か未来か
・元金が増減するかどうか
・年金に乗じる金額かどうか
この3つの特徴を使って6つの係数を分類すると下記のようになります。
| 係数の名称 | 知りたい金額 | 元金の増減 | 乗じる対象 |
|---|---|---|---|
| 終価係数 | 未来 | なし | ー |
| 現価係数 | 現在 | なし | ー |
| 年金終価係数 | 未来 | 増加 | 年金 |
| 減債基金係数 | 現在 | 増加 | ー |
| 年金現価係数 | 現在 | 減少 | 年金 |
| 資本回収係数 | 未来 | 減少 | ー |
このように分類した理由をこれから解説しますので、今は意味がわからなくて問題ありません!
それでは早速、3つの特徴の1つめの意味から解説していきます。
知りたい金額は現在か未来か
まず、6つの係数問題のお決まりのパターンを確認しておきましょう。
6つの係数問題の「お決まりの型」とは
6つの係数問題には「お決まりの型」があります。
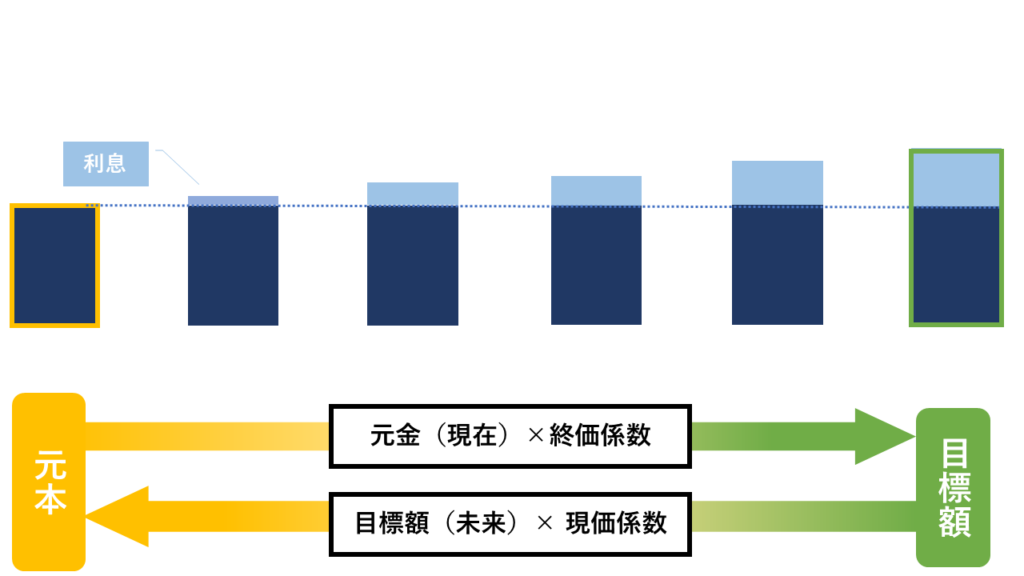
ある「資金運用計画」があって、その計画には既に「決まっている金額」と、これから「知りたい金額」があるというものです。
「知りたい金額を計算するために、決まっている金額に、何ていう名前の係数を掛け算するのか」というのが、6つの係数問題で問われる知識になります。
例えば「10年後に一定額を貯めるために必要な元本を求める」という場合、「決まっている金額」は10年後の目標額、「知りたい金額」は今から投資する元本になります。
知りたい金額は「現在」か「未来」か
「決まっている金額」が「未来の目標額」である場合、「知りたい金額」は必然的にそれを達成するため「今必要な元本」になります。
逆に「今から運用する元本」が「決まっている」場合、「知りたい金額」は、それを運用した後の「未来でもらえる額」になります。
「知りたい金額」と「決まっている金額」は必ずどちらかが「今(現在)」で、どちらかが「未来」の金額になります。
| 決まっている金額 | 知りたい金額 |
|---|---|
| 未来の目標額 | 今必要な元本 |
| 今から運用する元本 | 未来でもらえる額 |
6つの係数では「知りたい額」が「現在」である場合に使う係数が3つ、「未来」である場合に使う係数が3つに分かれています。
次の表をご覧ください。
| 係数の名称 | 知りたい金額 |
|---|---|
| 終価係数 | 未来 |
| 現価係数 | 現在 |
| 年金終価係数 | 未来 |
| 減債基金係数 | 現在 |
| 年金現価係数 | 現在 |
| 資本回収係数 | 未来 |
ここで表の、マーカーを引いた4つの係数の名称をよく見てください。
係数の名称に「現価」や「終価」の文字が使われています。
これを利用して、6つのうち4つの係数の「未来」と「現在」を簡単に覚える方法があります。
「現」は現在を求める係数、「終」は未来を求める係数
「知りたい金額」が「現在」である場合は、未来の金額に「現価」の文字が入っている係数を乗じます。
この知識があれば、次の問題を解くことができます。
【例】:10年後に100万円を貯めるために、今必要な元本を求める係数は「100万円×〇〇係数」である。
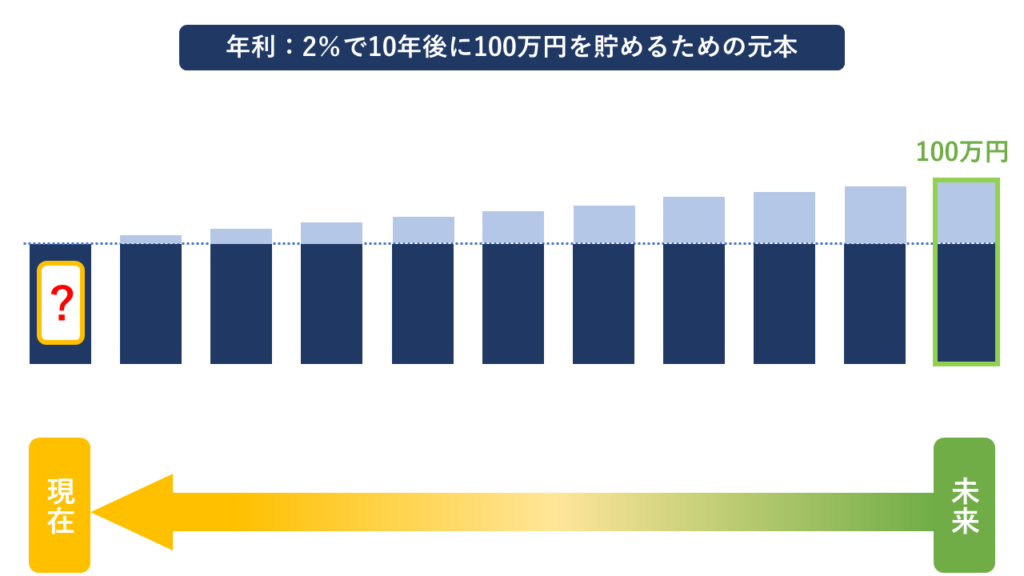
この問題の答えは「現価係数」です。
おすすめの覚え方は「現価=現化」です。何となく「現在」と覚えてしまうと、何に乗じる係数だったかを忘れるため、「現価=現化」で現在に向かっているイメージ(未来の金額に乗じて現在に向かって時をさかのぼっていくイメージ)を持つことをおすすめします。
「知りたい金額」が「未来」である場合は、現在の金額に「終価」の文字が入っている係数を乗じます。
【例】:100万円を10年間運用した後の元金と利息の合計は「100万円×〇〇係数」である。

この問題の答えは「終価係数」です。
おすすめの覚え方は「終価」→「終化」です。現在の金額から、目標である未来に向かっていくイメージです。
問題文から未来・現在を読み取ってみよう
それでは実際の過去問で、「知りたい金額」が現在か未来かを読み取ってみましょう。
下記は、2023年9月のFP2級の学科試験の問題です。

(出典):日本FP協会 2級ファイナンシャル・プランニング技能検定学科試験2023年9月
この1~4のそれぞれの選択肢の文章を読んで、求めたい金額が「現在」なのか「未来」なのかを読み取ってみましょう。
係数の名前が正しいかどうかは後からわかるようになります。ここでは「現在」と「未来」の判別に集中しましょう。
さっそく【選択肢1】から見ていきます。
【選択肢1】一定の利率で複利運用しながら一定期間経過後の元利合計額を試算する際、現在保有する資金の額に乗じる係数は、終価係数である
「~を試算する際」とあるので、この「~」のところが、求めたい金額です。
この問題では「一定期間経過『後』の元利合計額」を求めようとしています。
決まっている金額は「元本」、知りたい金額は将来の金額ですので、この問題は「未来」を求める係数が解答であることが読み取れます。
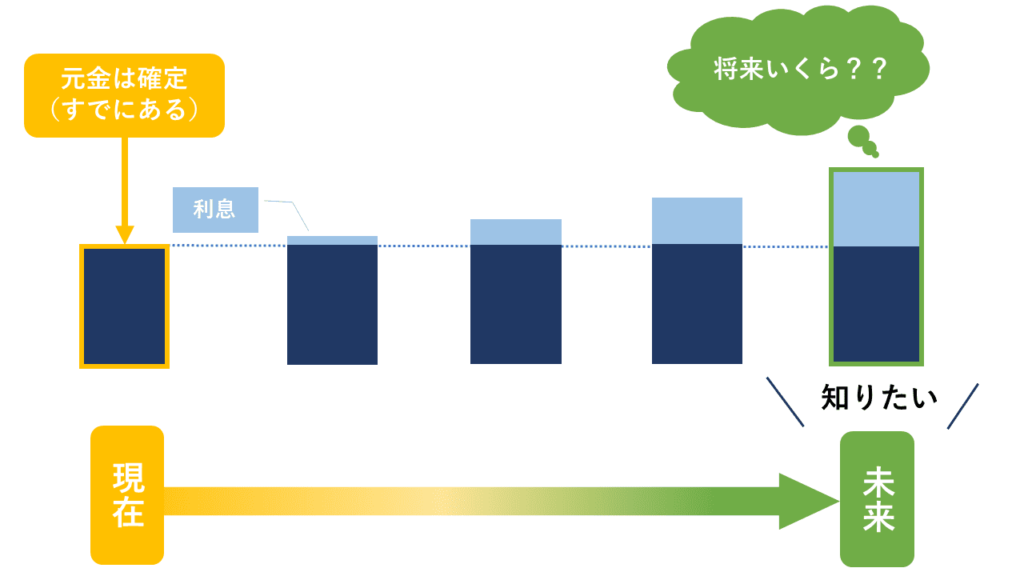
問題文では、「現在保有する資金の額」を運用するものとし、元金はすでに決まっていることを示しています。そして知りたい金額は運用後の「未来」ですので、「未来」を求める係数が解答になることを判別できます。
続いて【選択肢2】です。
【選択肢2】一定の利率で複利運用しながら一定期間、毎年一定金額を積み立てた場合の一定期間経過後の元利合計額を試算する際、毎年の積立額に乗じる係数は、年金終価係数である。
この問題でも、求めたい金額は「一定期間経過後の元利合計額」です。「将来の金額を知りたがっている」という状況が読み取れますので、未来になります。
【選択肢1】との違いは、「決まった年金額を積み立てる」という話であることです。
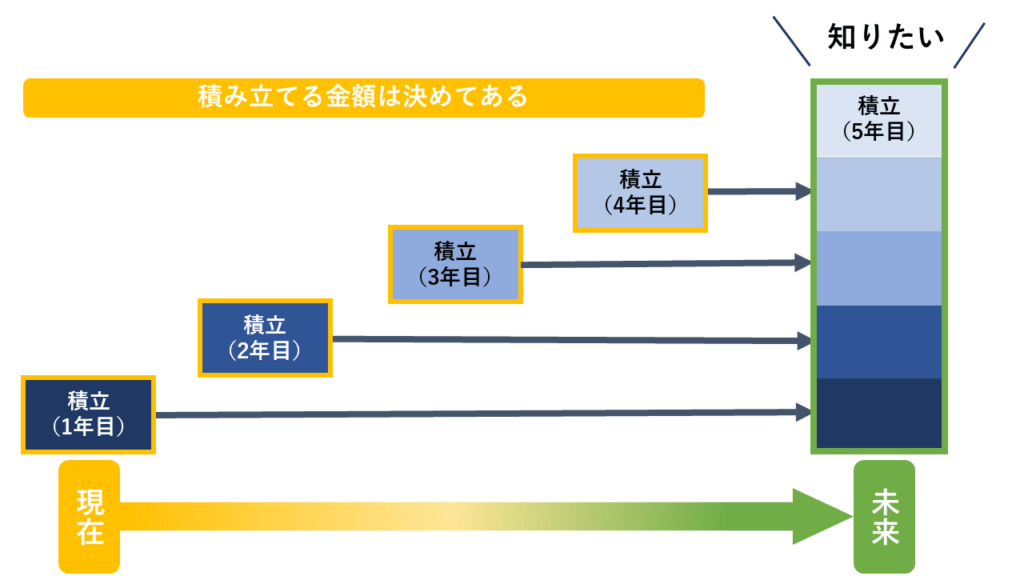
続いて【選択肢3】です。
【選択肢3】一定の利率で複利運用しながら一定期間、毎年一定金額を受け取るために必要な元本を試算する際、毎年受け取りたい金額に乗じる係数は、資本回収係数である。
この問題で求めたい金額は「必要な元本」です。
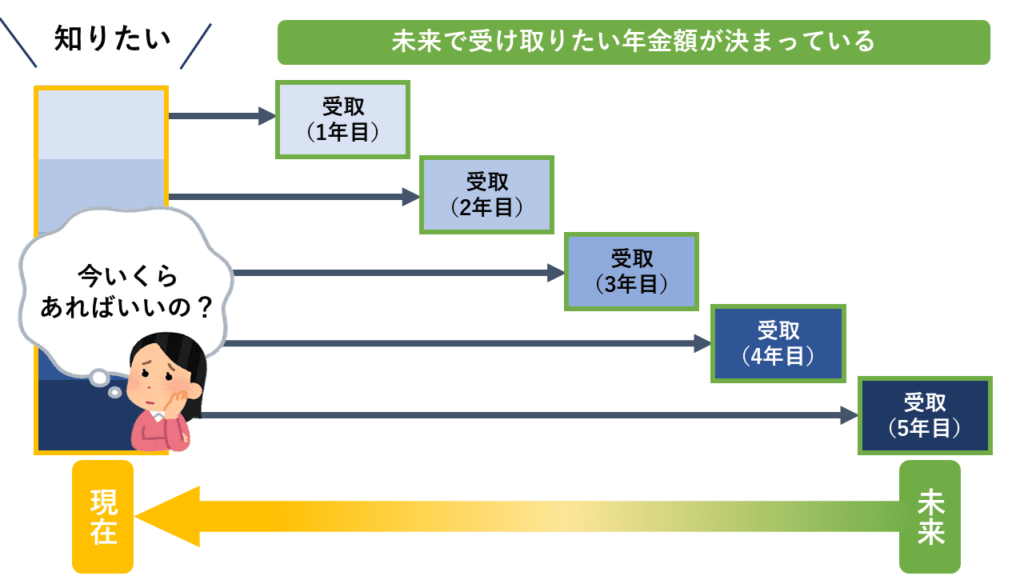
「未来で受け取りたい年金額」が決まっている人が「それを受け取るために今いくら元金があればいいのかが知りたい」ということを読み取ることがポイントになります。
したがって答えは「現在」です。
次のような図をイメージすることで、現在と未来の時間軸がわかりやすくなります。
次が最後です。
【選択肢4】一定の利率で複利運用しながら一定期間経過後に目標とする額を得るために必要な毎年の積立額を試算する際、目標とする額に乗じる係数は、減債基金係数である。
この問題の求めたい金額は「毎年の積立額」です。これも難しい問題ですが、よく出ます。
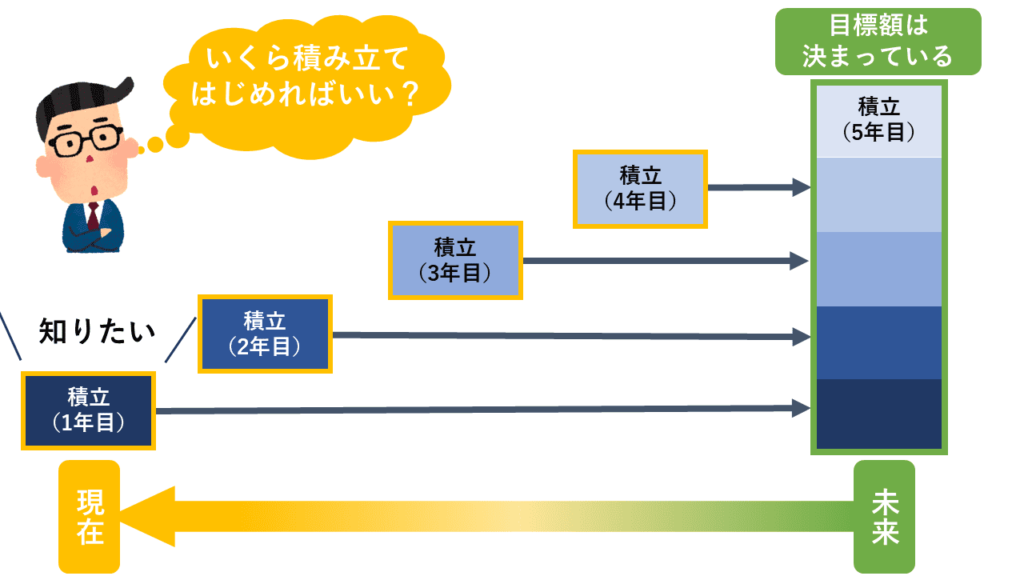
これは「未来で貯めたい目標額」が決まっている人が、それを貯めるために「今からいくら積み立てればよいか」を知りたがっていることを読み取れるかどうかがポイントです。
答えは「現在」です。
「未来の目標額」に対し、「積立額」はそれよりも前の、「現在側」の時間軸にあると気がつくことができれば答えがでます。
慣れるまでは次のような図を思い浮かべて「毎年の積立額」の時間軸が「現在」であることをイメージしましょう。
現在と未来が逆になっている選択肢を見つけてみよう
まだ説明の序盤なのですが、「現在」と「未来」の区別ができるようになっただけで、選択肢を絞れることがあります。
次は、2022年1月のFP3級の学科試験の問題です。
元金を一定の利率で複利運用しながら、毎年一定金額を一定の期間にわたり取り崩していくときの毎年の取崩し金額を計算する場合、元金に乗じる係数は、( )である。
1) 現価係数
2) 減債基金係数
3) 資本回収係数
(出典):日本FP協会3級ファイナンシャル・プランニング技能検定学科試験2022年1月
まずは、「知りたい金額」を読み取りましょう。
「~を計算する際」の「~」のところが、知りたい金額です。
したがって、これは元金が決まっている人が「これから毎年いくら取り崩せるか」を知りたがっているものです。
イメージ図は次のようになります。
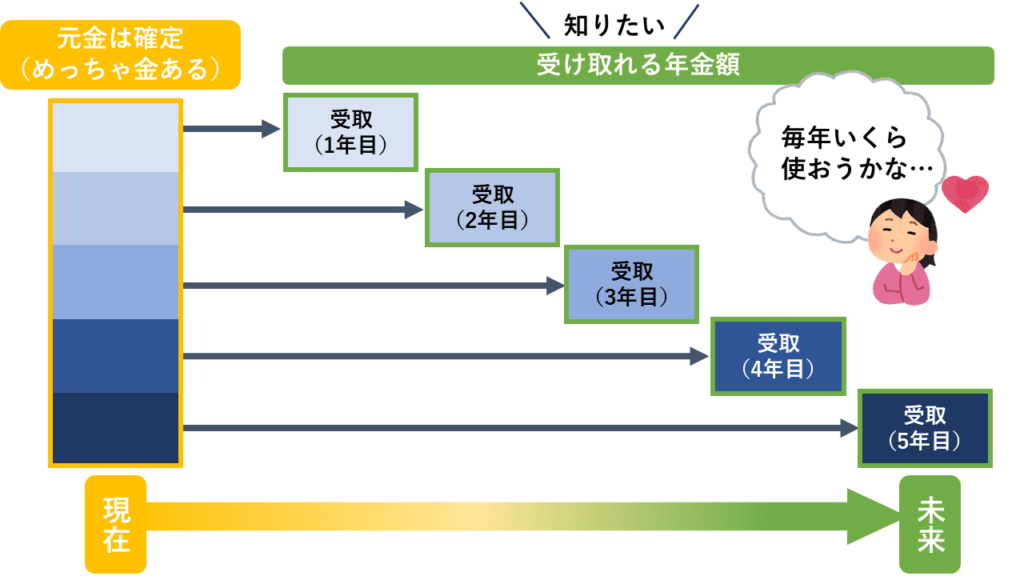
決まっている額(元金)に対して知りたい金額(受取れる額)はそれよりも後の、「未来側」の時間軸にあります。
つまり、この問題の解答は「未来」を求める係数でなければなりません。
そうすると、選択肢にある「現価係数」は「現在」を求める係数であるため、除外することができます。
ちなみに答えは、(3)の資本回収係数になります。
資本回収係数については後半で説明します。
もう一度みるなら
元金が増減するかどうか
続いては、「元金が増減するかどうか」で係数を覚える方法を紹介します。
6つの係数には、元金が途中で変動しない時に使うものが2つ、変動する時に使うものが4つあります。
| 係数の名称 | 求めたい金額 | 元金の増減 |
|---|---|---|
| 終価係数 | 未来 | なし |
| 現価係数 | 現在 | なし |
| 年金終価係数 | 未来 | 増加 |
| 減債基金係数 | 現在 | 増加 |
| 年金現価係数 | 現在 | 減少 |
| 資本回収係数 | 未来 | 減少 |
元金が途中で変動するかどうかとは、運用期間中に元本の増減があるかどうかです。「毎年積み立てる」とか「毎年受け取る・取り崩す」というような元本の増減が問題文に示されているものを意味します。
元金の変動がなければ、「終価係数」か「現価係数」のどちらかで確定です。
先ほど「現在・未来」の判別をした2級の問題文から、今度は元金の変動があるかないかを見分けてみましょう。
過去問から元本の増減を読み取ってみよう
先ほど、現在と未来の判別をしたFP2級の選択肢1~4で、今度は元本の増減を読み取りましょう。
【選択肢1】一定の利率で複利運用しながら一定期間経過後の元利合計額を試算する際、現在保有する資金の額に乗じる係数は、終価係数である
この問題文は、どこにも「毎年積み立てる」とか「毎年受け取る(取り崩す)」という表現がありません。
したがって、元本の増減は「なし」です。
この問題で知りたい金額は「未来」ですので、答えは「終価係数」で確定です。
【選択肢2】一定の利率で複利運用しながら一定期間、毎年一定金額を積み立てた場合の一定期間経過後の元利合計額を試算する際、毎年の積立額に乗じる係数は、年金終価係数である。
問題文に「毎年一定金額を積み立てた場合」とあるため、これは元本の増減「あり」です。
【選択肢3】一定の利率で複利運用しながら一定期間、毎年一定金額を受け取るために必要な元本を試算する際、毎年受け取りたい金額に乗じる係数は、資本回収係数である。
問題文に「毎年一定金額を受け取る」とあるため、これは元本の増減「あり」です。
【選択肢4】一定の利率で複利運用しながら一定期間経過後に目標とする額を得るために必要な毎年の積立額を試算する際、目標とする額に乗じる係数は、減債基金係数である。
問題文に「毎年の積立額」とあるため、これは元本の増減「あり」です。
元本の増減がないなら「四文字係数」
「毎年積み立てる」「毎年受け取る・取り崩す」というような文言が一切ないものは、終価係数か現価係数の2つの係数のいずれかになります。
覚え方は、6つの係数のうち、終価係数と現価係数のみが「四文字」であることです。たったの四文字で、とってもシンプルですよね。「四文字→シンプル→単純→元本の増減がない」といった連想で覚えましょう。
それでは、問題の選択肢から元本の増減があるのに四文字係数を使っているものを見つけて、選択肢を絞ってみましょう。
ここでは2つ問題を見ていきます。まずは、2021年5月のFP3級の学科試験の問題です。
一定の利率で複利運用しながら一定期間経過後に目標とする額を得るために必要な毎年の積立額を試算する際、目標とする額に乗じる係数は、( )である。
1) 現価係数
2) 資本回収係数
3) 減債基金係数
(出典):日本FP協会3級ファイナンシャル・プランニング技能検定学科試験2021年5月
こちらの問題は、積み立てがあることから、四文字係数である選択肢(1)を解答から消去して2択に絞ることができます。
ちなみに答えは(3)の減債基金係数です。
続いて、2023年1月のFP3級の学科試験の問題です。
元金を一定期間、一定の利率で複利運用して目標とする額を得るために、運用開始時点で必要な元金の額を試算する際、目標とする額に乗じる係数は、( )である。
1) 現価係数
2) 減債基金係数
3) 資本回収係数
(出典):日本FP協会3級ファイナンシャル・プランニング技能検定学科試験2023年1月
こちらの問題は、元金の変動がありません。したがって、四文字係数である選択肢(1)現価係数が解答になります。
【おさらい】
仮に選択肢に終価係数もあったとしましょう。この問題では目標額が決まっており知りたい金額が現在の必要な元金であると読み取れます。したがって、現価係数であると判断できます。
元本の増減がある場合
「毎年積み立てる」「毎年受け取る・取り崩す」という文言があれば、元本の増減があります。
したがって、四文字の係数を除いた、次の4つのいずれかになります。
| 係数の名称 | 求めたい金額 | 元金の増減 |
|---|---|---|
| 年金終価係数 | 未来 | 増加 |
| 減債基金係数 | 現在 | 増加 |
| 年金現価係数 | 現在 | 減少 |
| 資本回収係数 | 未来 | 減少 |
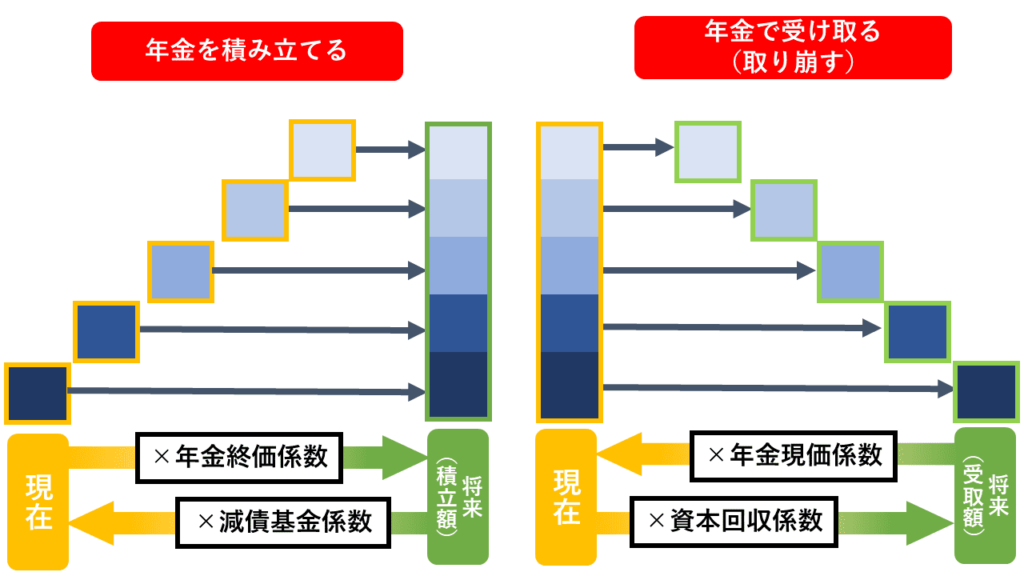
「積み立てる」場合は元金が増加し、「受け取る(取り崩す)」場合は元金が減少します。
そして「知りたい金額」が現在か未来かで、次のようになります。
もう一度みるなら
年金に乗じる係数かどうか
元本の増減のある4つの係数のうち、先に「年金終価係数」「年金現価係数」を覚えます。
「年金終価係数」「年金現価係数」の覚え方は簡単です。どちらも必ず「年金に乗じる係数」であるからです。
年金に乗じるのは「年金〇〇係数」だけ
元金が変動する問題は、毎年一定額を積み立てて増やしていくか、毎年一定額を受け取りながら元金を崩していく問題しかありません。
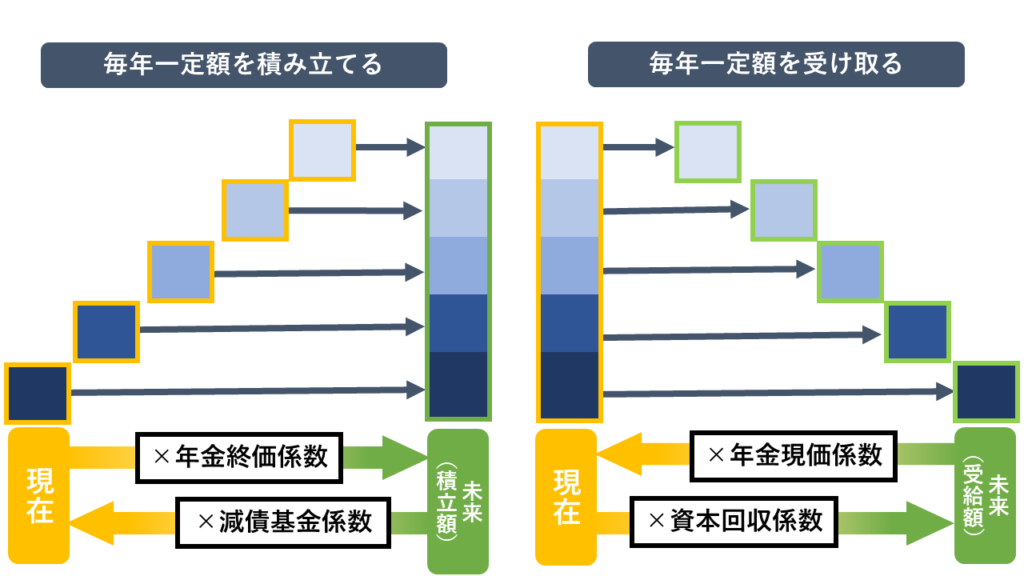
毎年一定額を積み立てて元金を増やしていく問題です。上り階段のような図で表現することができます。
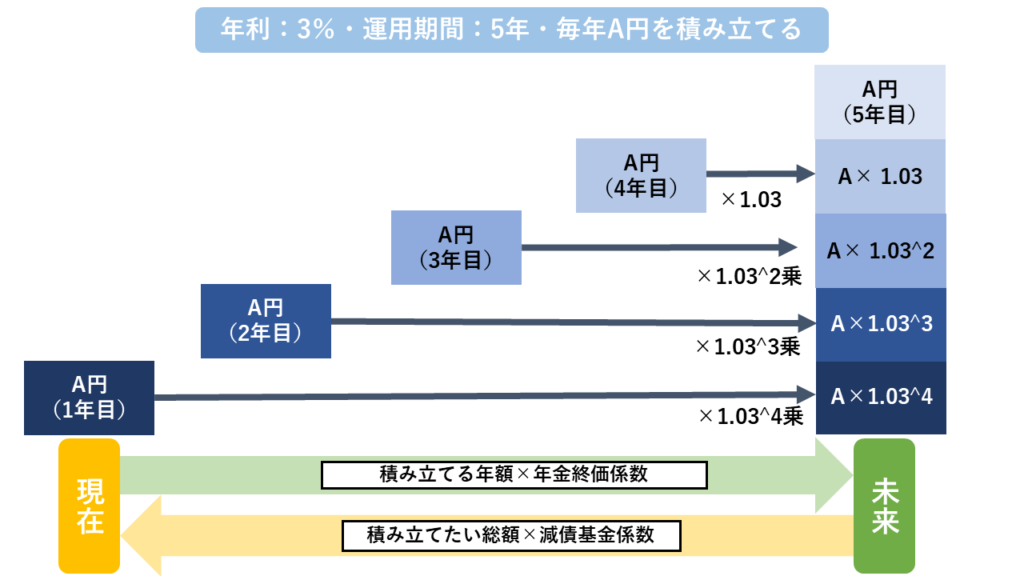
毎年積み立てる年金の額が問題文で決まっている場合は積み立て後(未来)の金額を年金終価係数で、積み立て目標額が決まっている場合はこれから積み立てる年金額(現在)を減債基金係数で求めます。
毎年一定額を受け取って元金を崩していく問題です。下り階段のような図で表現することができます。
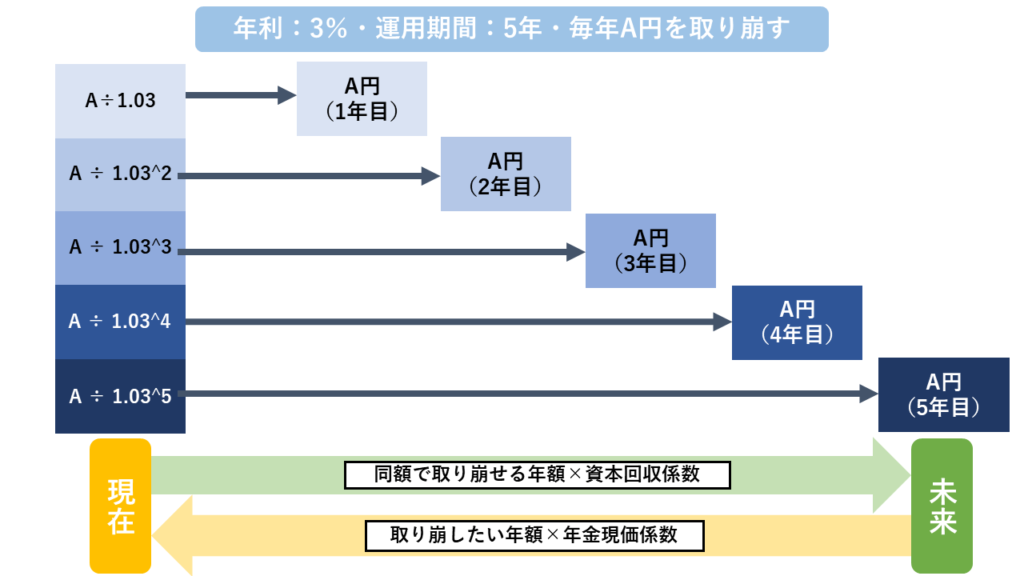
取り崩す前の現在の元金が問題文で決まっている場合は取り崩す(受け取る)金額を資本回収係数で、受け取りたい金額が決まっている場合は元金を年金現価係数で求めます。
ここから覚え方を解説します。4つの係数を一つにした図を再度みてみましょう。

まず4つの係数のうち「年金終価係数」は「終価」の文字どおり、未来の金額を求めるものです。
反対に「年金現価係数」は現在の金額を求めるものになります。
そしてこの「年金〇〇係数」は、かならず年金(1年あたりの金額)に乗じる係数になります。
つまり、こういうことです。
・積み立てる年金の額が決まっている場合(知りたいのは、年金積み立て後の額)
→ 1年あたりの積み立て額に年金終価係数を乗じる
・取り崩す年金の額が決まっている場合(知りたいのは、取り崩す前の元金)
→ 1年あたりの受け取り額に年金現価係数を乗じる
そして、ここまで見てきた「現在と未来」の区別、「元本の増減」の区別、そして今回の「年金に乗じるのは『年金〇〇係数』だけ」という3つを覚えていれば、ある1パターンの問題を除いて、すべて正答できます。
最後の1パターンについては、この後に解説します。まずは「年金に乗じるのは『年金◯◯係数』だけ」のルールに集中しましょう。
年金に「年金〇〇係数」を乗じていない選択肢を見つけてみよう
それでは「年金額に乗じるのは年金〇〇係数だけ」という知識で選択肢を絞ってみましょう。
最初に出題したFP2級の問題のうち、残りの【選択肢2~4】を解きます。誤っている選択肢が1つあります。
【選択肢2】一定の利率で複利運用しながら一定期間、毎年一定金額を積み立てた場合の一定期間経過後の元利合計額を試算する際、毎年の積立額に乗じる係数は、年金終価係数である。
【選択肢3】一定の利率で複利運用しながら一定期間、毎年一定金額を受け取るために必要な元本を試算する際、毎年受け取りたい金額に乗じる係数は、資本回収係数である。
【選択肢4】一定の利率で複利運用しながら一定期間経過後に目標とする額を得るために必要な毎年の積立額を試算する際、目標とする額に乗じる係数は、減債基金係数である。
このうち、間違っているのは【選択肢3】です。
【選択肢3】に、わざわざ「毎年受け取りたい金額に乗じる係数」と書いてくれているので、「毎年受け取る一定額=年金である」ことさえ読み取ることができれば、年金に乗じる「年金〇〇係数」の出番であるとわかります。
したがって、資本回収係数はありえません。
もう一度みるなら
減債基金係数と資本回収係数の覚え方
ここまでは6つの係数を3つの特徴で覚える方法を見ていきました。
(3つの特徴:①求める金額が現在か未来か、②元本の増減があるか、③年金に乗じるか否か)
最後に対策をしておきたいのが、元本が増減する係数の残りの2つである、減債基金係数と資本回収係数の覚え方です。この2つを入れ替えた選択肢がでても解けるよう対策する必要があります。
減債基金係数・資本回収係数とは
減債基金係数と資本回収係数は、「年金〇〇係数」とは逆に「1年あたりの積み立て額・受け取り額」を求める係数です。
一方が積み立て額の計算に使う係数で、もう一方が受け取り額の計算に使う係数になります。

減債基金係数と資本回収係数は、言葉のイメージで覚えるか、語呂合わせで覚える方法がおすすめです。
順に解説しますので、覚えやすいものをお使いください。
言葉のイメージで覚える方法
減債基金係数は「基金」という言葉から、国民年金基金や厚生年金基金といった、「年金を積み立てる」ことをイメージして覚えるようにします。
資本回収係数は、「受け取っていく(取り崩していく)=回収されていく」ことをイメージして覚えましょう。

資本回収係数は、投下した資本(投資額)を利息つきで回収する際の係数です。FP試験によくでる「取崩し」以外にも、ローンの返済年額を計算するときに用いられます。
・減債基金→毎年積み立てる
・資本回収→毎年回収する
なお「資本回収係数」は、自分のお金を運用しながら毎年取り崩す場合のほか、銀行などが顧客にお金を貸し、それを利息付きで毎年一定額を返済(元利均等返済)してもらう場合、年にいくら回収できるかを計算する時にも使います。
つまり、元本(資本)が将来いくらずつ返済されるか(いくらずつ回収できるか)を計算する係数です。
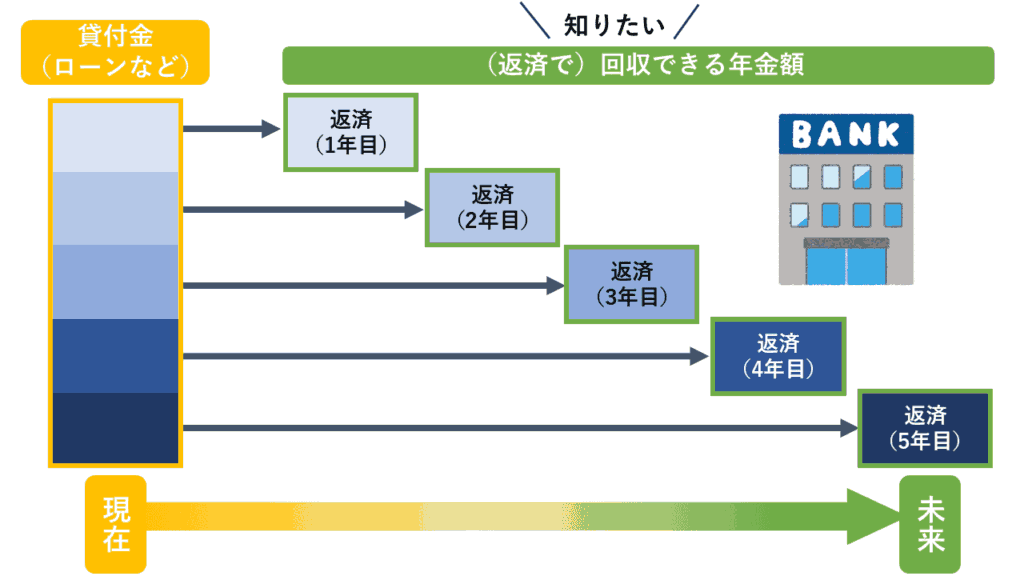
このことから「資本回収係数」とは、もともとは金融機関や投資家などの目線でネーミングされたものなのでしょう。
語呂合わせで覚える方法
減債基金係数は、「現在」を求める係数ですから、「減債」(ゲンサイ)と「現在」の語呂合わせで覚えることができます。
また、資本回収係数は「未来(終価)」を求める係数ですから、「回収」(カイシュウ)と「終」の音の一致で覚えることもできます。

・減債(ゲンサイ)→現在(ゲンザイ)
・減債基金→現在(現価)
・資本回収→未来(終価)
先頭の文字(減)と最後尾の文字(収)がポイントです!
どうしても思い出せない時の対策
減債基金係数と資本回収係数は、どちらか1つをしっかり覚えていれば「年金◯◯係数」の図解から消去法で導き出すこともできます。
もし試験中に思い出せなくなったら、とりあえず手を動かして、下記のように上り階段と下り階段の図を描いてみましょう。
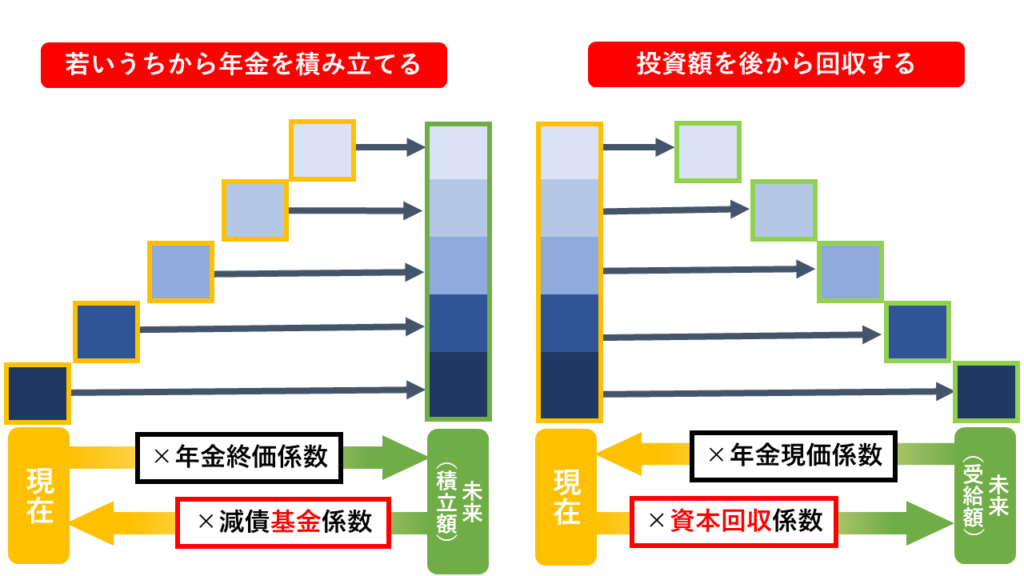
まずは年金終価係数・年金現価係数を書き込み、そこに減債基金係数と資本回収係数のどちらか思い出せるほうを書き込むことで、もう一つの係数を特定する方法もあります。
もう一度みるなら
総まとめ
最後に、ここまでの内容の総まとめと演習問題を行います。
6つの係数の覚え方の一覧表
| 係数の名称 | 知りたい金額 | 元金の増減 | 乗じる対象 |
|---|---|---|---|
| 終価係数 | 未来 | なし | ー |
| 現価係数 | 現在 | なし | ー |
| 年金終価係数 | 未来 | 増加 | 年金 |
| 減債基金係数 | 現在 | 増加 | ー |
| 年金現価係数 | 現在 | 減少 | 年金 |
| 資本回収係数 | 未来 | 減少 | ー |
・現価は現在、終価は未来
・元本の増減がない(=シンプル)なら、係数もシンプルな四文字
・年金に掛け算するのは「年金〇〇係数」
・減債は現価、回収は終価
演習問題
ここまでの話を振り返りながら、最初に出題したFP2級の問題のうち【選択肢1~4】を解いてみましょう。
【選択肢1】一定の利率で複利運用しながら一定期間経過後の元利合計額を試算する際、現在保有する資金の額に乗じる係数は、終価係数である
知りたい金額は「一定期間経過後の元利合計額」、つまり未来の金額です。また、元本の増減を示す言葉はありません。
答えは「終価係数」で「〇」です。
【選択肢2】一定の利率で複利運用しながら一定期間、毎年一定金額を積み立てた場合の一定期間経過後の元利合計額を試算する際、毎年の積立額に乗じる係数は、年金終価係数である。
知りたい金額は「一定期間経過後の元利合計額」、つまり未来の金額です。
また、「毎年一定金額を積み立てた場合」という条件から、元本の増加があることがわかります。
さらに、すでに決まっている金額は「毎年の積立額」であるため、求める係数は、年金に乗じる「年金〇〇係数」であることがわかります。
以上から、答えの係数は、年金の積み立て額から未来の金額を求める「年金終価係数」ですので、この選択肢は「〇」です。
【選択肢3】一定の利率で複利運用しながら一定期間、毎年一定金額を受け取るために必要な元本を試算する際、毎年受け取りたい金額に乗じる係数は、資本回収係数である。
知りたい金額は「必要な元本」、つまり「現在の金額」です。
また、「毎年一定金額を受け取る」という条件から、元本の減少があることがわかります。
さらに、すでに決まっている金額は「毎年受け取りたい金額」であるため、求める係数は、年金に乗じる「年金〇〇係数」であることがわかります。
以上から、答えの係数は、年金の受け取り額から今必要な元本を求める「年金現価係数」ですので、この選択肢は「✕」です。
【選択肢4】一定の利率で複利運用しながら一定期間経過後に目標とする額を得るために必要な毎年の積立額を試算する際、目標とする額に乗じる係数は、減債基金係数である。
知りたい金額は「必要な毎年の積立額」、つまり「現在の金額」です。
また、「毎年の積立額」という条件から、元本の増加があることがわかります。
さらに、すでに決まっている金額は「一定期間経過後に目標とする額」であるため、答えの係数は「年金◯◯係数」ではなく、減債基金係数か資本回収係数になります。
問題文で知りたい金額は「現在」なので語呂合わせで「減債(ゲンサイ)」あるいは、知りたい金額は「積立額」なので言葉のイメージから「基金」を連想することで「減債基金係数」であることがわかります。この選択肢は「〇」です。
もう一度みるなら
6つの係数の逆数関係について
ここでは、FP試験のテキストによくある6つの「逆数関係」について解説します。必要性は高くないため、余裕のある方だけ読み進めてください。
FP試験のテキストには、よく「6つの係数は、それぞれが逆数関係にある」という説明があると思います。
実はこの説明は、ここまでの6つの係数の覚え方をマスターすれば、ほぼ必要ありません。
かつては「係数あり」の解答に必要だった
かつては、この係数がなければ解けない問題がありました。
それは、係数の値が与えられる「係数あり」の問題のうち、問題文に3つの係数しか与えない問題です。
解答には、問題文で与えられていない係数を使用する必要があり、受験者は、必要な係数を「逆数関係」を使って自ら算定する必要がありました。
しかし、最近の「係数あり」の問題は、6つの係数がすべて与えられているものしか見かけません。
したがって、重要度は低いと思います。
筆者が確認できる範囲では、2018年のFP1級の学科試験(きんざいが実施する学科試験)で、問題文の資本回収係数の値から、年金現価係数を計算させて解答させる出題がありました。
もしあの悪夢のような問題を再開させるとしたらFP1級試験だと思います。FP1級を受験される方は、余裕があれば、逆数関係も覚えておくとよいかも知れません。
6つの係数の逆数関係
それでは、6つの係数の逆数関係を図解で見ていきましょう。
とはいえ、実はここまでの説明で「逆数関係」を意識した図解を使用しているので、実はもうマスターできているはずです。
だから、図解でイメージする必要があったんですね。
例えば、元本を年利2%で3年運用する場合に使用する「終価係数」は「約1.061」(=1.02^3乗)です。
この時、解答に必要な係数が「現価係数」であれば、「1÷1.02^3乗」をして「約0.9423」を自力で計算しなければなりません。端数処理は問題文にしたがいます。
残りの4つの係数の関係は、次のようになります。
表にまとめると下記のとおりです。
| 現価係数 | 終価係数 |
| 年金現価係数 | 資本回収係数 |
| 減債基金係数 | 年金終価係数 |
1級対策の演習をこちらの記事の後半に掲載しました。逆数関係を使う方法も解説していますのでご活用ください。
もう一度みるなら
直前でも間に合う!全級一発合格者がおすすめする問題集
FP3級から1級の試験をすべて一発合格した筆者は、すべての受験でTACの「あてるシリーズ」を直前に解いています。1級・2級・3級に分かれているので、受験する級のものを選ぶ必要があります。
「あてるシリーズ」は全3回分の予想問題が入った模試になります。
「〇年〇月試験」のようにおおむね試験ごとに予想問題が更新されているので、狙われやすい法改正にも完全対応しています。
おすすめのポイントは、価格の割に問題の質が高いことです。体感的には10点~20点くらいこの問題集で底上げできたと思います。
特に1級は合格点ギリギリでしたから、本当に感謝しています。
迷っている方は、問題集の「的中実績」を参考にしてください。
問題集を開いてすぐのページに、それまでの「的中実績」が大体いつも書かれています。PCであれば、Amazonの「試し読み」から「的中実績」のページを確認できます。
的中実績を見れば、おすすめする理由がきっと伝わると思います。商品名に偽りなしです。
言い換えると、ここまで的中しているものなので「この問題集でそこそこ点が取れないと本番もやばい」という目安になります。
おすすめのテキストも紹介しています。
ここまで読んでくださりありがとうございました。
もう一度みるなら



